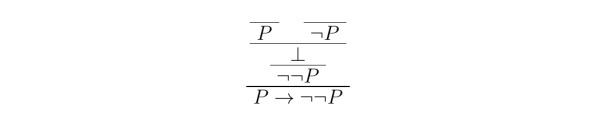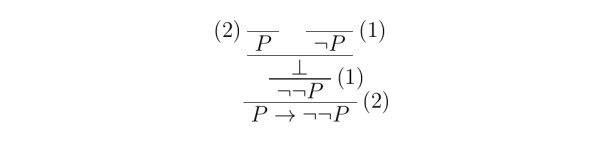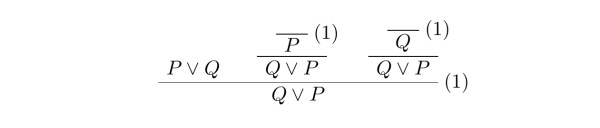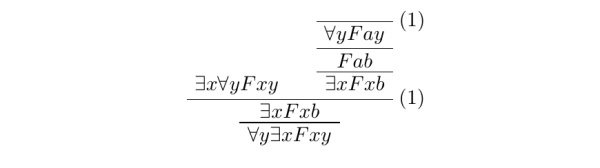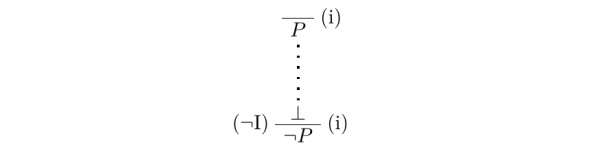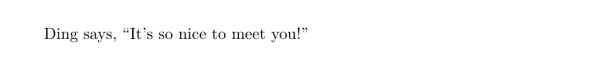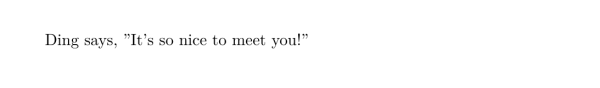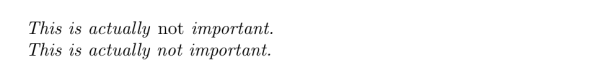用 LaTeX 写最基本的哲学论文
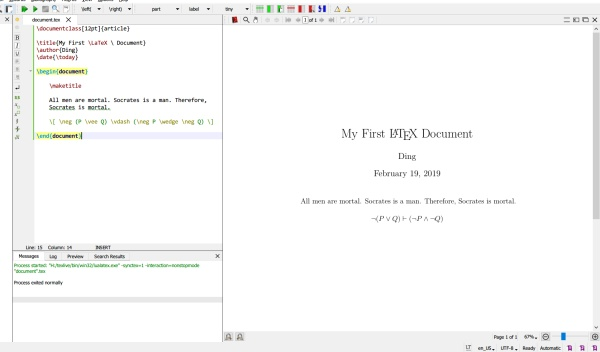
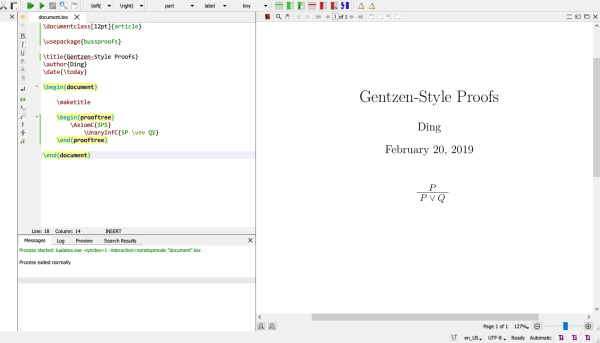
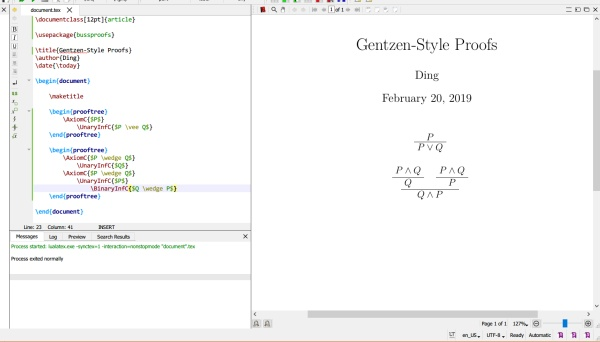
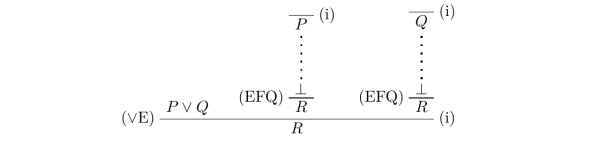
通过前几期教程,我们已经做出了第一份 \LaTeX 文档、会写根岑式证明了。是时候在 \LaTeX 上写我们的第一篇哲学论文辣~
引号
这可能是最需要去习惯的地方了。请将左双引号写成两个左撇号 ``(键盘左上角有波浪线的那个键),把右双引号写成两个单撇号 ‘’(英文输入法下的引号键)。单引号依此类推。
Ding says, ``It's so nice to meet you!''
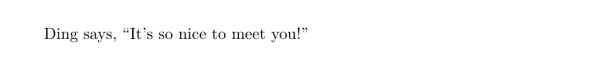
虽然现在的 \TeX 编辑器大多能识别 Unicode 下带方向的 “ 和 ”,一定要写 “ 和 ” 也不见得会出错了,但至少至少不要写不带方向的 " ——出错几乎不可避免:
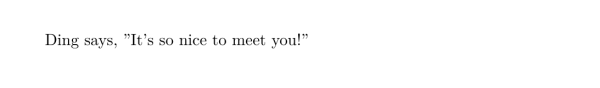
段落与换行
此外还需要特别注意的是空行的使用。我们已经习惯了 Word 等其它文字处理器中回车=新段落的规范:
I have something awesome to say here.
And something else as awesome!
但在 \LaTeX 中,这并不会生成新段落:
\text{I have something awesome to say here. And something else as awesome!}
我们所需要做的是,是回两次车,或者说真正地在中间空一行:
I have something awesome to say here.
And something else as awesome!
\begin{multline} \shoveleft \text{I have something awesome to say here.}\\ \shoveleft \text{And something else as awesome!} \end{multline}
这可能也是个需要习惯的地方,但熟悉 Markdown 语法的读者对此应该不会太陌生。事实上,若读者将来想要配合使用 git,那么最好的习惯是每句话写完后都回车一次,每段话写完后回车两次(即保留一个真正的空行):
All men are mortal.
Socrates is a man.
Therefore, Socrates is mortal.
Hey, it's valid and sound!
(注意这里句子与句子之间不需要再加空格——$\LaTeX$ 会处理好的。)
\begin{multline} \shoveleft \text{All men are mortal. Socrates is a man. Therefore, Socrates is mortal.}\\ \shoveleft \text{Hey, it's valid and sound!} \end{multline}
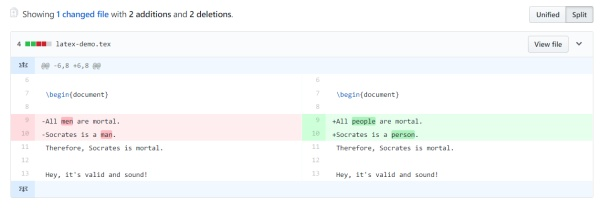
这种写作习惯会使 git 的使用变得非常便利:
强调、斜体和粗体
强调、斜体和粗体的语法分别是:
\emph{Emphasize your text}
\textit{Italicize your text}
\textbf{Bold your text}

在大部分时候,强调和斜体所生成的效果是一样的。但使用强调的好处主要在于它允许嵌套:
\emph{This is actually \emph{not} important.}
\textit{This is actually \textit{not} important.}
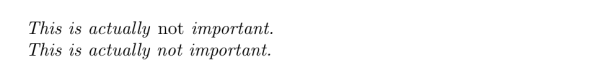
注意中间那个「not」的区别。
(很多编辑器都支持快捷键。例如在 TeXstudio中,强调是 Ctrl+Shift+E ,斜体是 Ctrl+I ,粗体是 Ctrl+B 。)
各种破折号
在英文中,我们区分三种长度不同的「破折号」:
-
连字符(hyphen) :用于连接单词,形式是 - ,如 Frankfurt-style counter-examples;
-
连接号(en dash) :用于连接时间/空间,形式是 – ,如 1891–1970;
-
破折号(em dash) :类似于汉语里的破折号,形式是 — 。
这三种不同的「破折号」分别用不同数量的 - 来书写:
Hyphen -
En dash --
Em dash ---

例子:
Frankfurt-style cases---introduced by Harry Frankfurt (1929--) in his 1969 essay ``Alternate Possibilities and Moral Responsibility''---are counter-examples to the Principle of Alternate Possibilities (PAP).

前提—结论形式
在书写哲学论文时,我们时常会需要把论证表达成前提—结论的形式:
- 如果月球是巧克力做的,那么特朗普就不是美国总统。
- 特朗普是美国总统。
- 所以,月球不是巧克力做的。(否定后件)
最简单的方法是采用有序列表,语法是:
\begin{enumerate}
\item Your first item...
\item Your second item...
\item Your third item...
\end{enumerate}
例如:
Here is Ding's argument for why the moon is not made of chocolate, in a premises-conclusion form:
\begin{enumerate}
\item If the moon is made of chocolate, then Trump is not the President of the United States.
\item Trump is the President of the United States.
\item Therefore, the moon is not made of chocolate.
\end{enumerate}

由于本文的目标仅仅是写出最基本的哲学论文,我们将在今后介绍如何把「P」「Q」等记号加进编号中,以及如何在中途打断列表插入正文。
章节
我们可以使用下面的命令创建章节:
\section{Name of Your Section}
\subsection{Name of Your Subsection}
\subsubsection{Name of Your Subsubsection}

例子:
\section{Ding's Argument}
Here is Ding's argument for why the moon is not made of chocolate, in a premises-conclusion form:
\begin{enumerate}
\item If the moon is made of chocolate, then Trump is not the President of the United States.
\item Trump is the President of the United States.
\item Therefore, the moon is not made of chocolate.
\end{enumerate}
\section{My Objection}
I argue that (1) of Ding's argument is false.
Obviously, (1) is false \emph{iff} the moon is made of chocolate and Trump is the President of the United States.
It is obviously true that the moon is made of chocolate, and that Trump is the President of the United States.
Thus, (1) is false.

脚注
脚注的语法如下:
\footnote{Here goes your footnote.}
例如:
Here is Ding's argument for why the moon is not made of chocolate, in a premises-conclusion form:
\footnote{This is my reconstruction of Ding's argument.}

引用
当然,最简单的方法是人肉写引用格式。(我们会在以后的教程中学习 BibLaTeX 等工具。)
Here is Ding's (2019, 121) argument for why the moon is not made of chocolate...

并人肉写结尾的参考文献目录(如果不想要 section 前面的编号,可以使用 \section*{} ):
\section*{References}
Ding. 2019. ``Trump, Moon and Chocolate.'' \emph{Zhihu Review of Philosophy} 9 (1): 117--123.

完整示例文档
\documentclass{article}
\title{My Objection to Ding's Argument}
\author{Dong}
\date{\today}
\begin{document}
\maketitle
In this paper, I will provide an objection to Ding's argument against a chocolate moon.
\section{Ding's Argument}
Here is Ding's (2019, 121) argument for why the moon is not made of chocolate, in a premises-conclusion form:
\footnote{This is my reconstruction of Ding's argument.}
\begin{enumerate}
\item If the moon is made of chocolate, then Trump is not the President of the United States.
\item Trump is the President of the United States.
\item Therefore, the moon is not made of chocolate.
\end{enumerate}
\section{My Objection}
I argue that (1) of Ding's argument is false.
Obviously, (1) is false \emph{iff} the moon is made of chocolate and Trump is the President of the United States.
It is obviously true that the moon is made of chocolate, and that Trump is the President of the United States.
Thus, (1) is false.
\section*{References}
Ding. 2019. ``Trump, Moon and Chocolate.'' \emph{Zhihu Review of Philosophy} 9 (1): 117--123.
\end{document}